:Yana:ZZZ: Economy (2010-12-11)
-
���Ѥȳ�Ψʬ�� (2010-06-11)
- ��Ū (2007-09-11)
- ����ʬ�ۤȡֺǰ��� (2007-09-11)
- ����ʬ�ۤ����� (2009-08-11)
- �п�����ʬ�ۤ����� (2009-12-11)
- �ե饯����ȥ٥�ʬ�� (2009-08-11)
- �Ȥꤢ�������б� (2009-10-11)
- �ϰϸ��� (2010-06-11)
-
���ѤȻ���ʬ (2010-12-11)
- ��Ū (2010-02-11)
- ������������ۤ����� (2010-10-11)
- ��ΨŪ�ե���ƥ��� (2010-12-11)
-
���Ѥȼ��� (2010-12-11)
- ��Ū (2007-07-11)
- ���� (2007-09-11)
- ��ԡʣ٣���ˤμ��� (2010-12-11)
-
���Ѥ���ɸ (2010-08-11)
- ��Ū (2008-01-11)
- ��ԡʣ٣���ˤ���ɸ (2009-06-11)
- ǯ��α��Ѥμ��� (2010-08-11)
-
���Ѥ��Ѹ� (2009-12-11)
- ��Ū (2007-10-11)
- ���Ѽ���Ψ�ȱ�����Ψ (2007-10-11)
- �����ȥꥹ�� (2009-12-11)
��Ū (2007-09-11)
���ѤˤĤ��ơ�������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤȳ�Ψʬ�ۤδط���Ƥ���ޤ���
����ʬ�ۤȡֺǰ��� (2007-09-11)
������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤ�����ʬ�ۤ����ꤹ�뤳�Ȥϡ�ͭ�ѤʤΤǤ��礦����
�ޤ����֥ۥ�ͤ�����פΡ֡ɥޥ͡����Ѵ��С�®������ֺ¡��ʣ��˺ǰ��Υ������ˤĤ��ơֶ�ۤǡ�����Ĥ��褦��������Ѥ��ޤ���
����ޤ��ˤϡ����ԥ������濴�Ȥ��ƾ岼����������ˣ������ޤ��岼�ˤ������Σ��ܤ��ϰ���Ǥ���У�����Υ������μ���Ψ�����������������������ꤵ��롣�Ĥޤꡢ��ǯ��˵����ꤦ�룹�������Ǻǰ��Υ��������ܽ�ϣ�.���飲��������Σ��ܤ�����ƥޥ��ʥ�����.����Ȥ������Ȥˤʤ롣����˰����������⤢������Τ����������Ψ���㤯�ʤ롣��ͻ�������Ǥϡ����Υޥ��ʥ���ɸ���к��Υ��������餤��ֺǰ��פȤ������ꤹ�뤳�Ȥ�¿����¾�λˤĤ��Ƥ�Ʊ�����Τǡֺǰ��ξ��פ����Ǥ��롣
�ޤ����ֻ��߷פؤ�ƻ�פΡ֥ܥ�ƥ���ƥ���´�������ˡ��������Ѥ��ޤ���
��ưΨ��ɸ���к�������뤳�Ȥǿ��Ͳ����뤳�Ȥ��Ǥ��ޤ������׳ؤ�����
�ˤʤ�ޤ���������ʬ�ۤ�����Ȥ����ʿ���ͤ���ץ饹�ޥ��ʥ���ɸ���к�
�����ȯ�������Ψ�Σ����������ޤ�ޤ����Ĥޤꤳ�γ�¦�ˤʤ��Ψ��
����ʲ��Ǥ����顢ɸ���к��Σ��ܤ���ư���ǰ��ξ������ꤷ�Ƥ���������
�������Ȥˤʤ�ޤ���
�����ǡ���ǯ�α�����Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤ���Ω������ʬ�ۡ�ʿ�ѡ��̡�ɸ���к����ҡˤ����ꤹ��ȡ���ǯ�α��Ѥǡ��̡ݦҰʾ�̡ܦҰʲ��ˤʤ��Ψ����������ʢ�ʣ������������ݣ������ˡߣ��ˤˡ��̡ݣ��Ұʾ�̡ܣ��Ұʲ��ˤʤ��Ψ����������ʢ�ʣ������������ݣ������ˡߣ��ˤˤʤ�ޤ���
�����ơ��̡ݣ��Ҥ�ֺǰ��פȤ���ȡ���ǯ�α��Ѥǡ��ֺǰ��װʾ�ˤʤ��Ψ����������ʢ⣰�����������ˤˤʤ�ޤ��������줬����³�����Ĥޤꡢ��ǯ�α��Ѥǡ��ֺǰ��װʾ夬³����Ψ����������ʢ⣰�������������ˤˤʤ�ޤ��������줬������³�����Ĥޤꡢ����ǯ�α��Ѥǡ��ֺǰ��װʾ夬³����Ψ����������ʢ⣰���������������ˤˤʤ�ޤ���������ϡ�����ǯ�α��Ѥǡ��ֺǰ��װʲ��ˣ���Ϥʤ��Ψ����������ʢ⣱�ݣ����������������ˤȤ������ȤǤ���
���Τ褦�ˡ�̤��α�����Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤ�����ʬ�ۤ����ꤹ��ȡ��̡ݣ��Ұʾ�ˤʤ��Ψ�ʤɤ���Ǥ��ޤ��������α�����Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤ�����ʬ�ۤʤΤǤ��礦����
����ʬ�ۤˤĤ��ơ��ֶ�ͻ���ؤΰ��⡡�٤���ʤ�����Υǥ�Хƥ��֤ȥݡ��ȥե��ꥪ������������ס����ԡ����ܲ�������������ǯ������������裱���裴���ˤΣ����ڡ���������Ѥ��ޤ���
�����ץ������ʤη���Ȥ����褯���Ѥ�����Ψʬ�ۤϡ�����ʬ�ۤ����ʬ�ۤ���ĤǤ�������������ʤɤθ����ʤ���̵�¤˺٤��ʻ��֤�ñ�̤Ȥ��ơ�̵�¤˺٤�������Ϣ³Ū���Ѳ���������ꤹ���ǥ�Ǥϡ������Ѳ�Ψ������ʬ�ۤˤ��������ȹͤ��뤳�Ȥ�¿�������������Ȥ��а�ʬ���Ȥ˰�����ߤ��Ѳ�����Ȥ����褦�ˡ�Υ��Ū���Ѳ������ꤹ���ǥ�Ǥϡ������Ѳ�Ψ�����ʬ�ۤˤ��������ȹͤ��뤳�Ȥ�¿���ΤǤ������Ԥ�����ʬ�ۤ�Ȥ���ǥ����ɽ���֥�å���硼�륺����ǥ�Ǥ������Τ˸����ȡ��п�����ʬ�ۤ��Ȥ��Ƥ��ޤ��ˡ�
�������ޤ��ˤߤ�ȡ����¤α������Ѳ�Ψ������ʬ�ۤ��������ʬ�ۤˤʤäƤ��ޤ��������������������Ӥ���ȡ�����ñ�̤�¬�ä������β����Ѳ�Ψ�ϡ�����ʬ�ۤˤϤʤäƤ��ޤ���Ʊ��ɸ���к���������ʬ�ۤ���٤Ƥߤ�ȡ����Ȥ��а����˻��߰ʾ���Ѳ�����ʤɤΡ���ü���礭���Ѳ����������Ψ�ϡ�����ʬ�ۤ��⸽�¤�ʬ�ۤ��������ʤ�⤤�ΤǤ����ޤ����ΰ����ǡ������δ֤ˤۤȤ���Ѳ����ʤ��Ȥ������ݤ��������Ψ�⡢���¤������⤤�ΤǤ����������ꡢ�椰�餤���Ѳ�Ψ���������Ψ�ϡ�����ʬ�ۤ���٤��㤤���Ȥˤʤ�ޤ����ĤޤꡢƱ��ɸ���к���������ʬ�ۤ���٤�ȡ����¤α������Ѳ��ϡ��Ȥ����礭���Ѳ������ꡢ�Ȥ����Ѳ����ʤ��ʤä��ꤹ��Ȥ��������ǡ��Ѳ�������ʤȤ��Ȱ��ꤷ�Ƥ���Ȥ��κ��������㤷���ΤǤ���
�����ǡ��ְ���ñ�̤�¬�ä������β����Ѳ�Ψ�פ�����ʬ�ۡʤ⤷�����п�����ʬ�ۡˤǤϤʤ����ֶ�ü���礭���Ѳ����������Ψ�פ�����ʬ�ۡʤ⤷�����п�����ʬ�ۡˤ���֤��ʤ�⤤�פȤ������ȤǤ��������֤���ѹ��������Ρֲ����Ѳ�Ψ�פ��ǧ�������Ȥ����Ǥ���
����ʬ�ۤ����� (2009-08-11)
����ʬ�ۤˤĤ��ơ��֤�������Ω������ʬ�ۡס����ԡ�̬ë����ɧ����������ǯ����������裱���ˤͤˤ��ơ��������ǧ���ޤ���
- �ѥ���
- �̡��ҡ䣰
- �ϰ�
- �ݡ������
- ��Ψ̩�ٴؿ�
- �ʡʣ��С��������ҡ��ݣ����ݡʣ��������ݣ��ʣ��ݦ̡���
- �����͡ʥ⡼�ɡ�
- ��
- ����͡���̿���
- ��
- ʿ�ѡʴ����͡�
- ��
- ʬ��
- ����
����ʬ�ۡ�ʿ�ѡ��̡�ʬ���������ˤ˽�����Ψ�ѿ��ؤ��Τ褦��ɽ�����Ȥˤ��ޤ���
�ء��Ρʦ̡������ˤΤȤ�����������������Ѥ�����Ψ�ѿ��١��ܣ�ؤϡ��١��Ρʣ�ܣ�̡����������ˤˤʤ�ޤ�������Ψ�ѿ��ڡ�ʣءݦ̡ˡ��Ҥϡ��ڡ��Ρʣ������ˤˤʤ�ޤ���
��Ψ�ѿ������ȳ�Ψ�ѿ���������Ω�ǡ��������Ρʦ������������ˤǡ��������Ρʦ������������ˤΤȤ�����������������������Ѥ�����Ψ�ѿ��١���������ܣ��������ϡ��١��Ρʣ��������ܣ����������������������ܣ������������ˤˤʤ�ޤ���
��Ψ�ѿ������ȳ�Ψ�ѿ���������Ω�ǡ��������Ρʣ������ˤǡ��������Ρʣ������ˤΤȤ�����Ψ�ѿ��١���������γ�Ψ̩�ٴؿ��ϡ����Τ褦�ˤʤ�ޤ��ʣ����ʣ��ˤϡ��護��ν����٥å���ؿ��סˡ�
- ���ݣ������ʡã��á�
- �����ʣ��ˡ�������ʣ��ܣ������ݣ���������ʣ����ˣ��
�����ǡ�������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤ�����ʬ�ۤ����ꤷ�Ƥߤޤ���
�㤨�С�������Ψ������ʬ�ۤ����ꤷ�ơ��̡ᣲ�Ȥ���ȡ�������Ψ�����ܤ��飲�ܤˤʤ��Ψ�ȣ��ܤ��飳�ܤˤʤ��Ψ��Ʊ���ˤʤ�ޤ���
�ޤ�������ʬ�ۤ��ϰϤϡݡ������Ǥ����������ϰϤγ�Ψ̩�ٴؿ��ϣ�����礭���Τǡ�������Ψ������ʬ�ۤ����ꤹ��ȡ�������Ψ������̤���ˤʤ��Ψ��������礭�����Ȥˤʤꡢ�ʸ���ۤ����Ȥ����٤ǡ˱�����Ψ�����ܰʾ�ˤʤ뱿�Ѥˤϻ��ѤǤ��ޤ���
�ޤ������Ѽ���Ψ������ʬ�ۤ����ꤹ��ȡ����Ѽ���Ψ���ݣ�������̤���ˤʤ��Ψ��������礭�����Ȥˤʤꡢ�ʸ���ۤ����Ȥ����٤ǡ˱��Ѽ���Ψ���ݣ�������ʾ�ˤʤ뱿�Ѥˤϻ��ѤǤ��ޤ���
���ˡ�ʣ���DZ��Ѥ������ˤĤ��ơ���Ω�ʳ�Ψ�ѿ����Ѥ���Ѥ��Ƥߤ�ȡ���Ψ�ѿ������ȳ�Ψ�ѿ���������Ω�ǡ��������Ρʣ������ˤǡ��������Ρʣ������ˤΤȤ�����Ψ�ѿ���������������γ�Ψ̩�ٴؿ��ϡ�����ʬ�ۤγ�Ψ̩�ٴؿ��ˤʤ�ޤ���Τǡ���Ψ�ѿ�����������ʬ�ۤ˽����ޤ���
�ޤ�����Ψ�ѿ������ȳ�Ψ�ѿ���������Ω�ǡ��������Ρʦ������������ˤǡ��������Ρʦ������������ˤΤȤ�����Ψ�ѿ��������������������ʬ�ۤ˽����Ȳ��ꤹ��ȡ����Τ褦�ʳ�Ψ�ѿ�������ʬ�ۤ˽������Ȥˤʤ�ޤ�������Ψ�ѿ�����������ʬ�ۤ˽����ޤ���Τǡ���Ψ�ѿ�����������ʬ�ۤ˽���ʤ����Ȥˤʤ�ޤ���
- �ʣ��������ݦ��������ݦ��������ܦ��������ˡ��ʦ��������ˡ�ʡʣ����ݦ����ˡ������ˡʡʣ����ݦ����ˡ�������
�Ĥޤꡢ����ǯ�ȼ���ǯ�α�����Ψ����Ω������ʬ�ۤ����ꤹ��ȡ����Σ�ǯ��ʣ���α�����Ψ������ʬ�ۤˤʤ�ޤ���
�ʤ���ñ���DZ��Ѥ������ˤĤ��ơ���Ω�ʳ�Ψ�ѿ����¤���Ѥ��Ƥߤ�ȡ���Ψ�ѿ������ȳ�Ψ�ѿ���������Ω�ǡ��������Ρʦ������������ˤǡ��������Ρʦ������������ˤΤȤ�����Ψ�ѿ��١�����ܣ����ݣ��ϡ��١��Ρʦ����ܦ����ݣ����������ܦ������ˤˤʤ�ޤ���
�Ĥޤꡢ����ǯ�ȼ���ǯ�α�����Ψ����Ω������ʬ�ۤ����ꤹ��ȡ����Σ�ǯ��ñ���α�����Ψ������ʬ�ۤˤʤ�ޤ���
�п�����ʬ�ۤ����� (2009-12-11)
�п�����ʬ�ۤˤĤ��ơ��֤�������Ω������ʬ�ۡס����ԡ�̬ë����ɧ����������ǯ����������裱���ˤͤˤ��ơ��������ǧ���ޤ���
- �ѥ���
- �̡��ҡ䣰
- �ϰ�
- ��������
- ��Ψ̩�ٴؿ�
- �ʡʣ��С��������ң����ݣ����ݡʣ��������ݦ̡������ʣ�������
- �����͡ʥ⡼�ɡ�
- ���̡ݦ���
- ����͡���̿���
- ����
- ʿ�ѡʴ����͡�
- ���̡ܣ��ݣ�����
- ʬ��
- �����̡ܦ����ʣ������ݣ���
��Ψ�ѿ��٤�����ʬ�ۡ�ʿ�ѡ��̡�ʬ���������ˤ˽����Ȥ�����Ψ�ѿ��ء�������п�����ʬ�ۤ˽����Ȥ��������Τ褦��ɽ�����Ȥˤ��ޤ���
��Ψ�ѿ������ȳ�Ψ�ѿ���������Ω�ǡ��������������Ρʦ������������ˤǡ��������������Ρʦ������������ˤΤȤ�����Ψ�ѿ��١���������ϡ��������١��Ρʦ����ܦ������������ܦ������ˤˤʤ�ޤ���
�����ǡ�������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤ��п�����ʬ�ۤ����ꤷ�Ƥߤޤ���
�㤨�С�������Ψ���п�����ʬ�ۤ����ꤷ�ơ��̡���������Ȥ���ȡ�������Ψ�����ܤ��飲�ܤˤʤ��Ψ�ȣ��ܤ��飴�ܤˤʤ��Ψ��Ʊ���ˤʤ�ޤ���
�ޤ����п�����ʬ�ۤ��ϰϤϣ�������Ǥ�����������Ψ���п�����ʬ�ۤ����ꤹ��ȡ�������Ψ�����ܰʲ��ˤ��б����ޤ���Τǡ��ʸ���ۤ����Ȥ����٤ǡ˱�����Ψ�����ܰʾ�ˤʤ뱿�Ѥˤϻ��ѤǤ��ޤ���
�ޤ������Ѽ���Ψ���п�����ʬ�ۤ����ꤹ��ȡ����Ѽ���Ψ������ʲ��ˤ��б����ޤ���Τǡ��ʸ���ۤ����Ȥ����٤ǡ˱��Ѽ���Ψ���ݣ�������ʾ�ˤʤ뱿�Ѥˤϻ��ѤǤ��ޤ���
���ˡ�ʣ���DZ��Ѥ������ˤĤ��ơ���Ω�ʳ�Ψ�ѿ����Ѥ���Ѥ��Ƥߤ�ȡ���Ψ�ѿ������ȳ�Ψ�ѿ���������Ω�ǡ��������п�����ʬ�ۤ˽������������п�����ʬ�ۤ˽����Ȥ�����Ψ�ѿ��١�����������п�����ʬ�ۤ˽����ޤ���
�Ĥޤꡢ����ǯ�ȼ���ǯ�α�����Ψ����Ω���п�����ʬ�ۤ����ꤹ��ȡ����Σ�ǯ��ʣ���α�����Ψ���п�����ʬ�ۤˤʤ�ޤ���
�ե饯����ȥ٥�ʬ�� (2009-08-11)
�ޤ����٥���§�ȥ٥�ʬ�ۤˤĤ��ơ��֥����Υե����å������Ծ������ʪ��ˡ§�ס����ԡ���½�������������ҡ���������ǯ��������������ǣ����ˤΣ������ڡ���������Ѥ��ޤ���
�٥���§��power law���ؿ������٥���ʣ����ˤ˽����褦��ˡ§���٥���ؿ��ϥ���������Ѥ����Ѵ��ʣ����ˣ��ˤƤ�ؿ������Ѳ����ʤ��Τǡ������̾��Ƥ�Ʊ���褦�˸�����ե饯������������Ū��ɽ�����뤳�Ȥˤʤ롣
�٥�ʬ�ۡ�power law distribution����Ψ̩�ٴؿ����٥���δؿ��˽����褦��ʬ�ۡ�����Ū�ˤϡ�ʿ���ͤ�����ɸ���к���̵���硤�Ȥ����褦�ʰ츫��̯�����������뤬��ʬ�ۤȤ��Ƥ����˶��������������롣����Ū�ˤϰ���ʬ�ۤΤ����Τ���ʬ���٥�ʬ�ۤˤʤäƤ���Τǡ��礭�ʤ����Τ���ʬ�ۤ˽����ѿ�������碌������dz�ĥ���줿�濴�˸������ˤ�äơ��٥�ʬ�ۤ��¸������롣
�ޤ������ʤ��Ѱ̤ˤĤ��ơ��֥����Υե����å������Ծ������ʪ��ˡ§�פΣ����ڡ���������Ѥ��ޤ���
�����ʤ��Ѱ̤�ʬ�ۤ��礭�ʤ����Τ����뤳�Ȥ�����Ū�Ǥ��äƤ⡤���δؿ����ޤ�����Ū���ɤ����ϡ��ޤ��Ϥä���ȤϤ��Ƥ��ʤ������ؤΥǡ����˴ؤ��Ƥϡ��٥���Ƕ������Ȼؿ��ϡݣ��������٤ˤʤ�Τ��Ф��������˴ؤ��Ƥϡ��˥塼�衼���Ծ������ʥǡ�������Ϥ�����̡��ؿ����ۤܡݣ��Υ٥�ʬ�ۤˤ�äơ��褯�������뤳�Ȥ���𤵤�Ƥ���������
�����ǡ����ʤ��Ѱ̤ǤϤʤ���������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤ�Ƥ�������Ȥ����Ǥ����������ѿ��ˤĤ��ơ��֥����Υե����å������Ծ������ʪ��ˡ§�פΣ����ڡ���������Ѥ��ޤ���
�����������ɽ���̣��Ȥ��Ƥϡ���������Ω����褦���̤ǡ�����Ū�ˤϼ����ѿ��Ȥ�Ф���Τ˸��ꤵ��롣���Ȥ��С��壱������ȿ売�����������碌��У�������ˤʤ�Τǡ����̤ϼ����ѿ��Ǥ��뤬��������ο�ȣ�����ο��Ʊ������碌�Ƥ⡤������Τ���ˤϤʤ�ʤ����Ȥ���狼��褦�ˡ����٤˴ؤ��Ƥ���������Ω���ʤ��Τǡ����٤ϼ����ѿ��ǤϤʤ����ܽ���о줹���̤Ȥ��Ƥϡ����Ȥ��С�ñ�̻��֤��������������̩�٤��Ȥ���ĹΨ�ʤɤϡ������ѿ��ǤϤʤ��������ѿ��Ȥ�Ф���̤Ǥ��롣���̤˥ե饯������Ϥ���ˤϡ������ѿ��������ѿ��Ǥ��뤫�ɤ�����ǽ�˹�θ���Ƥ����ʤ���Фʤ�ʤ���
������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤˤĤ��Ƥϡ����̤ʤɤμ����ѿ��ǤϤʤ�����Ȥ���ĹΨ�ʤɤμ����ѿ��Τ褦�Ǥ��Τǡ��ե饯����ǥ٥�ʬ�ۤȤ����ꤷ�ޤ�������ʬ�ۡʤ⤷�����п�����ʬ�ۡˤdz�ǧ���Ƥ���褦�ˡ��٥�ʬ�ۡʤ⤷�����п��٥�ʬ�ۡˤˤĤ��ơ���Ω�ʳ�Ψ�ѿ����Ѥʤɤ��ǧ�������Ȥ����Ǥ���
�Ȥꤢ�������б� (2009-10-11)
�ޤ���������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤˤĤ��ơ�̤���ʬ�ۤϤ狼��ޤ���
�㤨�С�����ʬ�ۡ�ʿ�ѡ��̡�ɸ���к����ҡˤ����ꤷ�ơ��̡ݣ��Ҥ�ֺǰ��פȤ���Τϡ�̤��Ρֺǰ��פ�ᾮɾ�����뤫�⤷��ޤ���
�ޤ�����������ʬ�ۤǤϡ�ʿ�Ѥ�ʬ�����������ޤ������Τ褦��ʬ�ۤ����ꤹ��ȡ�����ʬ��ʿ��ʬ�����ץ������ϻ��ѤǤ��ޤ���
���ˡ���ǯ�α�����Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤˤĤ��ơ�ʬ�ۤʤɤβ�������פdz�ǧ���Ƥ��顢���Ѥ˻��Ѥ���ˤϡ�������û�����⤷��ޤ���
�㤨�С���������ǯ�˥˥�������å��ǥɥ�ȶ�θ���ߤ���Ƥ��顢����ǯ�ˤʤ�ޤ�������ǯ�α��ѤȤ������ȤǤϡ�ɸ�ܤϣ����Ĥˤʤ�ޤ���
�ϰϸ��� (2010-06-11)
���ץ����Υ��顼�Ȥ������Ȥǡ���ͭ���Ƥ��븶�ˤĤ��ơ��ץåȤ���äƥ���������ȡ����β��¤Ⱦ�¤�����Ǥ���褦�Ǥ���
Ʊ�����ʤΥץåȤ���äƥ���������ȡ������������ȡ����顼�ˤʤ�ޤ���
������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤˤĤ��ơ�̤���ʬ�ۤϤ狼��ޤ������β��¤Ⱦ�¤����ꤷ������ʿ�Ѥ�ɸ���к����ǧ�������Ȥ����Ǥ���
��Ū (2010-02-11)
���ѤˤĤ��ơ�������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤȻ���ʬ�δط���Ƥ���ޤ���
������������ۤ����� (2010-10-11)
���ؤ˻��¤��Ƹ��Ƥ��뱿�ѼԤλ���ʬ��ͤ��Ƥߤޤ���
�¤�����ϻ��Ȼ¡��ξ�����֣��Ĥλ��ȣ��Ĥλ¤�ס����Ƥα��ѼԤ��¤����ι�פ��������ξ�����ֻ��θĿ��ϻ¤θĿ��Σ��ܡפȤ��ơ����ʤ飳���Ĥ�����������Ȼ¤���ʬ���ޤ���
������������ۤ�����
|
��
|
��
|
�ξ������ѹ����줿���
|
���ξ������ѹ����줿���
|
��������
|
������
|
������
|
��ʬ���ѹ����ʤ�
|
��ʬ���ѹ�����
|
����
|
������
|
������
|
��ʬ���ѹ�����
|
��ʬ���ѹ����ʤ�
|
����
|
������
|
������
|
��ʬ���ѹ����ʤ�
|
��ʬ���ѹ����ʤ�
|
�����ǡ�������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤˤĤ��ơ�������Ȥ���ȡ����Ƥα��ѼԤ��¤����ι�פ����Ǥ��Τǡ�������α��ѼԤ�������ˤϡ�����겼�α��ѼԤ����뤳�Ȥˤʤ�ޤ���
��������α��ѼԤϡ��ξ������ѹ����줿���Ǥ⡢����Ψ������Ʊ���Ǥ��Τǡ�����Ʊ��������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤˤʤ�ޤ��������ξ������ѹ����줿���Ǥ⡢����Ψ������Ʊ�ͤ��ѹ��Ǥ���С�����Ʊ��������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤˤʤ�ޤ���
���ۤ����̤α��ѼԤϡ�����Ψ�����Ȱۤʤ�ޤ��Τǡ����Ȱۤʤ뱿����Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤˤʤ�ޤ���
�ʤ�����������α��ѼԤ�������Ʊ��������Ψ�ʤ⤷���ϱ��Ѽ���Ψ�ˤˤʤ�Ȥ��Ƥ⡢̤��γ�Ψʬ�ۤϤ狼��ޤ����������뤳�Ȥ⤢��С����뤳�Ȥ⤢��Ǥ��礦��
�ޤ����㤨�С��������ѤȤ������ȤǤϡ��������㤬�������ۥ������ȡ����ۤ�����ۥ������ȡ����̤��������������Ȥˤʤ�褦�Ǥ���
�������ۥ������Ȥ�����ۥ������Ȥ���������������
|
�ξ������ѹ����줿���
|
���ξ������ѹ����줿���
|
�������ۥ�������
|
��ʬ���ѹ����ʤ�
|
��ʬ���ѹ�����
|
����ۥ�������
|
��ʬ���ѹ�����
|
��ʬ���ѹ����ʤ�
|
��������������
|
��ʬ���ѹ����ʤ�
|
��ʬ���ѹ����ʤ�
|
��ΨŪ�ե���ƥ��� (2010-12-11)
���Ѽ���Ψ�ˤĤ��ơ�̤��γ�Ψʬ�ۤϤ狼��ޤ���ʿ�Ѥ�ɸ���к�����ط������������ʤ����⤷��ޤ���������������ꤷ�ơ����ʿ�Ѥ���������ɸ���к����������Ȼ����ط����������Ȥ��ơ�����ʬ��ͤ��Ƥߤޤ���
����Ψ�ˤĤ��ơ���ˣ�������ʬ���ơ��������ᣱ�Ȥ���ȡ���פ������Ѽ���Ψ��ʿ�Ѥ�ɸ���к��ϡ����Τ褦�ˤʤ�ޤ���
��פ������Ѽ���Ψ��ʿ�Ѥ�ɸ���к�
|
��פ������Ѽ���Ψ��ʿ��
|
��פ������Ѽ���Ψ��ɸ���к�
|
���Ȼ¤���ʬ�������
|
���������ܣ�������
|
�ʣ������������ܣ������������������������ܣ�������������������
|
�����ʬ�������
|
����������
|
�ʦ��������������������������������
|
�����ǡ���ط������ϰϤϡݣ��������壱�Ǥ�������ط�������̤���ξ��ˤϡ���פ������Ѽ���Ψ�ˤĤ��ơ�Ʊ��ʿ�ѤǤ���С�ɸ���к����������ʤ�褦����ʬ�������Ȥ����Ǥ��������Τ褦�ʥ��եȥ���������Ѥ��ޤ���
�㤨�С����Τ褦�ʻˤĤ��ơ���פ������Ѽ���Ψ��ʿ�Ѥ�ɸ���к�����Ǥ��ޤ�����
ʿ�Ѥ�ɸ���к�����ط���
|
ʿ��
|
ɸ���к�
|
��ط���
|
��
|
��
|
��
|
��
|
����
|
������
|
��
|
�ݣ�����
|
��
|
��
|
������
|
������
|
�ݣ�����
|
��
|
������
|
��
|
������
|
������
|
��
|
������
|
��
|
ʿ�Ѥ��ѿ���m�פ�ɸ���к����ѿ���s�פ���ط������ѿ���p�פ���Ѥ��Ƥ��ޤ���
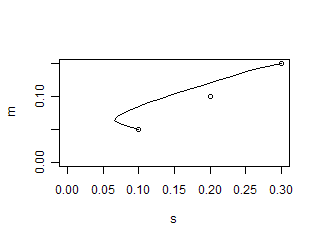
# (C) 2010 Yana
library(tseries)
m <- c(.05, .1, .15)
s <- c(.1, .2, .3)
p <- matrix(c(1, -.5, 0, -.5, 1, .5, 0, .5, 1), length(m))
plot(s, m, xlim = c(0, max(s)), ylim = c(0, max(m)))
y <- seq(min(m), max(m), length.out = 16)
x <- c()
for (i in y) {
j <- portfolio.optim(t(m), i, covmat = s %*% t(s) * p)
x <- c(x, sqrt((j$pw * s) %*% t((j$pw * s) %*% p)))
}
lines(x, y)
��Ū (2007-07-11)
���ѤˤĤ��ơ�ɾ���ۤʤɤΥǡ������顢���ӤȤ��Ƥα�����Ψ������ޤ���
���� (2007-09-11)
�ޤ����������ɽ�����եȡפȤ��ơ����Τ褦�ʥ��եȥ���������Ѥ��ޤ���
���ˡ�����ۤ�ɾ���ۤʤɤΥǡ��������Ϥ��ޤ���
�ǡ���������
|
A
|
B
|
C
|
1
|
ɾ����
|
�����
|
ɾ����
|
2
|
2004-12-31
|
10
|
20
|
3
|
2005-03-31
|
11
|
22
|
4
|
2005-06-30
|
12
|
24
|
������Ǥϡ����Ѥ�����ɲä��ơ�����ۤ����䤷�Ƥ��ޤ��������Τ褦�ʸ��������ۡʥ���å��塦�ե����ˤαƶ���ޤޤʤ����ֲýż���Ψ�ͤˤ��ơ����������Ϥ��ޤ���
���ա����������ۡʥ���å��塦�ե����ˤαƶ���ޤ��۲ýż���Ψ�ˤϡ��б����Ƥ��ޤ���
����������
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
1
|
ɾ����
|
�����
|
ɾ����
|
���鷿������Ψ
|
������������Ψ
|
���ѱ�����Ψ
|
ǯ���ʿ�ѱ�����Ψ
|
2
|
2004-12-31
|
10
|
20
|
|
|
1
|
|
3
|
2005-03-31
|
11
|
22
|
=C3/(C2-B2+B3)
|
=(C3+B2-B3)/C2
|
=F2*MIN(D3;E3)
|
=(F3/F$2)^(365.2425/(A3-A$2))
|
4
|
2005-06-30
|
12
|
24
|
=C4/(C3-B3+B4)
|
=(C4+B3-B4)/C3
|
=F3*MIN(D4;E4)
|
=(F4/F$2)^(365.2425/(A4-A$2))
|
�����ǡ��ģ��δ��鷿������Ψ�ϣ�����ɾ������ľ��ˡ��ţ��δ�����������Ψ�ϣ�����ɾ������ľ���ˡ����Ѥ�����ɲä������α�����Ψ�ˤʤ�ޤ���
�����ơ��ƣ������ѱ�����Ψ�Ǥϡ��ģ��δ��鷿������Ψ�ȣţ��δ�����������Ψ�ξ����������ͤ���Ѥ��Ƥ��ޤ���
���ա����鷿������Ψ�ȴ�����������Ψ�ˤĤ��ơ�ʬ�Ҥ�ʬ�줬���ʲ��ξ��ˤϡ��б����Ƥ��ޤ���
�������
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
1
|
ɾ����
|
�����
|
ɾ����
|
���鷿������Ψ
|
������������Ψ
|
���ѱ�����Ψ
|
ǯ���ʿ�ѱ�����Ψ
|
2
|
2004-12-31
|
10
|
20
|
|
|
1
|
|
3
|
2005-03-31
|
11
|
22
|
1.048
|
1.050
|
1.048
|
1.208
|
4
|
2005-06-30
|
12
|
24
|
1.043
|
1.045
|
1.093
|
1.197
|
�ʤ������Ѥ����︺���ơ�����ۤ餹���ˤ⡢Ʊ����������Ѥ��ޤ���
�������
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
1
|
ɾ����
|
�����
|
ɾ����
|
���鷿������Ψ
|
������������Ψ
|
���ѱ�����Ψ
|
ǯ���ʿ�ѱ�����Ψ
|
2
|
2004-12-31
|
10
|
20
|
|
|
1
|
|
3
|
2005-03-31
|
9
|
18
|
0.947
|
0.950
|
0.947
|
0.803
|
4
|
2005-06-30
|
8
|
16
|
0.941
|
0.944
|
0.892
|
0.793
|
�ޤ�������ۤǤϤʤ������������ۡʥ���å��塦�ե����ˤ����Ϥ�����ˤϡ��̤ο�������Ѥ��ޤ���
����������
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
1
|
ɾ����
|
����������
|
ɾ����
|
���鷿������Ψ
|
������������Ψ
|
���ѱ�����Ψ
|
ǯ���ʿ�ѱ�����Ψ
|
2
|
2004-12-31
|
|
20
|
|
|
1
|
|
3
|
2005-03-31
|
1
|
22
|
=C3/(C2+B3)
|
=(C3-B3)/C2
|
=F2*MIN(D3;E3)
|
=(F3/F$2)^(365.2425/(A3-A$2))
|
4
|
2005-06-30
|
1
|
24
|
=C4/(C3+B4)
|
=(C4-B4)/C3
|
=F3*MIN(D4;E4)
|
=(F4/F$2)^(365.2425/(A4-A$2))
|
�������
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
1
|
ɾ����
|
����������
|
ɾ����
|
���鷿������Ψ
|
������������Ψ
|
���ѱ�����Ψ
|
ǯ���ʿ�ѱ�����Ψ
|
2
|
2004-12-31
|
|
20
|
|
|
1
|
|
3
|
2005-03-31
|
1
|
22
|
1.048
|
1.050
|
1.048
|
1.208
|
4
|
2005-06-30
|
1
|
24
|
1.043
|
1.045
|
1.093
|
1.197
|
�������
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
1
|
ɾ����
|
����������
|
ɾ����
|
���鷿������Ψ
|
������������Ψ
|
���ѱ�����Ψ
|
ǯ���ʿ�ѱ�����Ψ
|
2
|
2004-12-31
|
|
20
|
|
|
1
|
|
3
|
2005-03-31
|
-1
|
18
|
0.947
|
0.950
|
0.947
|
0.803
|
4
|
2005-06-30
|
-1
|
16
|
0.941
|
0.944
|
0.892
|
0.793
|
��ԡʣ٣���ˤμ��� (2010-12-11)
�������
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
1
|
ɾ����
|
�����
|
ɾ����
|
���鷿������Ψ
|
������������Ψ
|
���ѱ�����Ψ
|
ǯ���ʿ�ѱ�����Ψ
|
2
|
2004-12-31
|
?
|
?
|
|
|
1
|
|
3
|
2005-03-31
|
?
|
?
|
1.017
|
1.018
|
1.017
|
1.073
|
4
|
2005-06-30
|
?
|
?
|
1.029
|
1.029
|
1.047
|
1.097
|
5
|
2005-09-30
|
?
|
?
|
1.035
|
1.036
|
1.084
|
1.113
|
6
|
2005-12-31
|
?
|
?
|
1.019
|
1.020
|
1.104
|
1.104
|
7
|
2006-03-31
|
?
|
?
|
1.005
|
1.005
|
1.109
|
1.087
|
8
|
2006-06-30
|
?
|
?
|
1.000
|
1.000
|
1.109
|
1.072
|
9
|
2006-09-30
|
?
|
?
|
1.030
|
1.031
|
1.143
|
1.079
|
10
|
2006-12-31
|
?
|
?
|
1.042
|
1.042
|
1.190
|
1.091
|
11
|
2007-03-31
|
?
|
?
|
1.010
|
1.010
|
1.202
|
1.086
|
12
|
2007-06-30
|
?
|
?
|
1.046
|
1.046
|
1.258
|
1.096
|
13
|
2007-07-31
|
?
|
?
|
0.984
|
0.984
|
1.238
|
1.086
|
14
|
2007-08-31
|
?
|
?
|
0.967
|
0.967
|
1.197
|
1.070
|
15
|
2007-09-30
|
?
|
?
|
1.034
|
1.034
|
1.239
|
1.081
|
16
|
2007-10-31
|
?
|
?
|
1.022
|
1.023
|
1.266
|
1.087
|
17
|
2007-11-30
|
?
|
?
|
0.955
|
0.955
|
1.210
|
1.068
|
18
|
2007-12-31
|
?
|
?
|
1.011
|
1.011
|
1.223
|
1.070
|
19
|
2008-01-31
|
?
|
?
|
0.946
|
0.945
|
1.156
|
1.048
|
20
|
2008-02-29
|
?
|
?
|
1.015
|
1.015
|
1.174
|
1.052
|
21
|
2008-03-31
|
?
|
?
|
0.960
|
0.959
|
1.126
|
1.037
|
22
|
2008-04-30
|
?
|
?
|
1.042
|
1.042
|
1.174
|
1.049
|
23
|
2008-05-31
|
?
|
?
|
1.014
|
1.014
|
1.190
|
1.052
|
24
|
2008-06-30
|
?
|
?
|
0.986
|
0.986
|
1.174
|
1.047
|
25
|
2008-07-31
|
?
|
?
|
0.987
|
0.987
|
1.158
|
1.042
|
26
|
2008-08-31
|
?
|
?
|
0.979
|
0.979
|
1.134
|
1.035
|
27
|
2008-09-30
|
?
|
?
|
0.927
|
0.927
|
1.051
|
1.013
|
28
|
2008-10-31
|
?
|
?
|
0.892
|
0.892
|
0.937
|
0.983
|
29
|
2008-11-30
|
?
|
?
|
0.963
|
0.963
|
0.903
|
0.974
|
30
|
2008-12-31
|
?
|
?
|
0.992
|
0.992
|
0.895
|
0.973
|
31
|
2009-01-31
|
?
|
?
|
0.971
|
0.971
|
0.869
|
0.966
|
32
|
2009-02-28
|
?
|
?
|
1.014
|
1.014
|
0.881
|
0.970
|
33
|
2009-03-31
|
?
|
?
|
1.041
|
1.042
|
0.918
|
0.980
|
34
|
2009-04-30
|
?
|
?
|
1.042
|
1.042
|
0.957
|
0.990
|
35
|
2009-05-31
|
?
|
?
|
1.048
|
1.048
|
1.002
|
1.001
|
36
|
2009-06-30
|
?
|
?
|
1.012
|
1.012
|
1.014
|
1.003
|
37
|
2009-07-31
|
?
|
?
|
1.016
|
1.016
|
1.030
|
1.006
|
38
|
2009-08-31
|
?
|
?
|
1.008
|
1.008
|
1.038
|
1.008
|
39
|
2009-09-30
|
?
|
?
|
1.003
|
1.003
|
1.041
|
1.009
|
40
|
2009-10-31
|
?
|
?
|
1.015
|
1.015
|
1.057
|
1.011
|
41
|
2009-11-30
|
?
|
?
|
0.979
|
0.979
|
1.034
|
1.007
|
42
|
2009-12-31
|
?
|
?
|
1.031
|
1.032
|
1.067
|
1.013
|
43
|
2010-01-31
|
?
|
?
|
0.980
|
0.980
|
1.045
|
1.009
|
44
|
2010-02-28
|
?
|
?
|
1.004
|
1.004
|
1.050
|
1.009
|
45
|
2010-03-31
|
?
|
?
|
1.050
|
1.050
|
1.102
|
1.019
|
46
|
2010-04-30
|
?
|
?
|
1.019
|
1.019
|
1.124
|
1.022
|
47
|
2010-05-31
|
?
|
?
|
0.929
|
0.929
|
1.044
|
1.008
|
48
|
2010-06-30
|
?
|
?
|
0.989
|
0.989
|
1.032
|
1.006
|
49
|
2010-07-31
|
?
|
?
|
1.026
|
1.026
|
1.058
|
1.010
|
50
|
2010-08-31
|
?
|
?
|
0.977
|
0.977
|
1.034
|
1.006
|
51
|
2010-09-30
|
?
|
?
|
1.041
|
1.041
|
1.077
|
1.013
|
52
|
2010-10-31
|
?
|
?
|
0.996
|
0.996
|
1.073
|
1.012
|
��Ū (2008-01-11)
���ѤˤĤ��ơ���ɸ���������ޤ���
��ԡʣ٣���ˤ���ɸ (2009-06-11)
���ѤȤ���¾�μ��٤�ͤ��Ƥߤޤ���
- �߱�����Ψ�ܱ��ѳ������ݱ��ѳ��ٽ�
̤��Τ��ȤϤ狼��ޤ�����ԡʣ٣���ˤξ��ˤϡ����ѳ����������ѳ��ٽФ��⾮�����ʤꤽ���Ǥ��Τǡ����Τ褦����ɸ�ͤˤ��ʤ��顢���Ѥ��Ƥ��ޤ���
- ������Ψ�ˤĤ��ơ�ǯ��α��Ѥμ���
- ���ѳ������ˤĤ��ơ��¶������
- ���ѳ��ٽФˤĤ��ơ�ʪ��������
�����ǡ�ǯ��Ȥ������ȤǤϡ���ԡʣ٣���ˤ��������Ƥ������ܹ�θ�Ūǯ��ʹ�̱ǯ��ȸ���ǯ��ˤ��ʤ��褦�˱��Ѥ������Ȥ����Ǥ���
�ޤ����¶��ʪ���Ȥ������ȤǤϡ���ԡʣ٣���ˤ����褷�Ƥ������ܹ���¶��ʪ�����ʤ��褦�˱��Ѥ������Ȥ����Ǥ���
�ʤ������Ѥ�������ɸ�ǤϤʤ������ѤȤ���¾�μ��٤���ɸ�Ȥ������ȤǤϡ����ѳ����������ѳ��ٽФ��⾮�����ʤäƤ⡢��︺���ʤ��褦�ˤ������Ȥ����Ǥ���
- �ߡʱ�����Ψ�ݣ��ˡܱ��ѳ������ݱ��ѳ��ٽС棰
ǯ��α��Ѥμ��� (2010-08-11)
ǯ��α��Ѥμ��ӤˤĤ��ơ����ֲýż���Ψ�ͤˤ��ޤ���
- ǯ����Ω�����������Ω����ˡ��
- ǯ����Ω�����������Ω����ˡ��
- ��ȸ�̳�������ȹ�Ϣ���
- ��ȸ�̳�������ȹ�Ϣ���internet
- ������̳�������ȹ�Ϣ���
- ������̳�������ȹ�Ϣ���
- ���ܻ�Ω�ع����������ѻ����ġ����ѻ�������
- ��ض��ѻ��ȡåȥåץڡ���
- ���ӵ������ο��������ȹ�
- ����ǯ��WebSite
- ��̱ǯ����Ϣ���
- ��̱ǯ����
- ���ǯ��Ϣ���
- ���ǯ��Ϣ���åȥåץڡ���
ǯ����Ω�����������Ω����ˡ�͡ʻԾ챿�ѻ����Ρˤȴ��ǯ��Ϣ�������ˤˤĤ��Ƥϡ����ֲýż���Ψ���ǧ�Ǥ��ޤ�����
���ֲýż���Ψ
|
ǯ����Ω�����������Ω����ˡ�͡ʻԾ챿�ѻ����Ρ�
|
���ǯ��Ϣ��������
|
��ԡʣ٣����
|
ʿ������ǯ��
|
14.37%
|
22.68%
|
9.04%
|
ʿ������ǯ��
|
4.56%
|
5.62%
|
8.38%
|
ʿ������ǯ��
|
-6.10%
|
-9.88%
|
-6.33%
|
ʿ������ǯ��
|
-10.04%
|
-18.37%
|
-18.51%
|
ʿ������ǯ��
|
9.58%
|
17.84%
|
20.10%
|
�ʤ���ǯ����Ω�����������Ω����ˡ�ͤȴ��ǯ��Ϣ���ˤĤ��ơ�ʿ������ǯ�٤λ������ǧ�Ǥ��ޤ�����
ʿ������ǯ�٤λ���
|
ǯ����Ω�����������Ω����ˡ��
|
���ǯ��Ϣ���
|
����ķ�
|
�Ծ챿��
|
50.79%
|
36.7%
|
�����
|
16.75%
|
�������
|
12.01%
|
17.1%
|
����ķ�
|
8.26%
|
20.2%
|
�������
|
10.79%
|
25.4%
|
û����
|
1.41%
|
|
��ư��
|
|
0.6%
|
��Ū (2007-10-11)
���ѤˤĤ��ơ��Ѹ���������ޤ���
���Ѽ���Ψ�ȱ�����Ψ (2007-10-11)
�ޤ������Ѽ���Ψ�ȱ�����Ψ�ˤϡ����Τ褦�ʴط�������ޤ���
- ���Ѽ���Ψ���ɾ���ۡݸ���ۡˡ������
- ������Ψ��ɾ���ۡ������
- �豿�Ѽ���Ψ�᱿����Ψ�ݣ�
���ˡ���ԡʣ٣���ˤϡ����Τ褦�ʲ����פ��Ĥ��ޤ�����
- ʣ�������ʿ�Ѥʤɤ��Ф��ơ�ñ�������ʿ�Ѥʤɤ���Ѥ��Ƥ��ޤ����Ȥϡ�������Ψ���Ɀ�Ѽ���Ψ������¿����
�㤨�С�����ǯ�α�����Ψ�����ܡ�����ǯ�α�����Ψ�����ܤȤ��ơ����Σ�ǯ��ʣ���α�����Ψ�������ȡ����������ܡʡᣰ�����ߣ������ˤˤʤ�ޤ�����������Ψ���Ѽ���Ψ���ѹ����ơ�����ǯ�α��Ѽ���Ψ��ݣ�������ǯ�α��Ѽ���Ψ��ܣ�����Ȥ��ơ����Σ�ǯ��ʣ���α��Ѽ���Ψ�������ȡ��ޣ���ʡ�ݣ������ܣ������ˤˤ��Ƥ��ޤ����Ȥ�¿�����Ȥ������ȤǤ���
�ޤ����֤���������ΤäƤ������������׳ءס����ԡ�����������ץ��롼�ס���������ǯ��������������裱���ˤΣ������ڡ���������Ѥ��ޤ���
�����Τ��Ȥ�Ƨ�ޤ��ơ����γ���������Ψ���ߤ�����Ω�Ȥ�������Ʊ�������ʬ�ۤ˽����Ȥ��ޤ������ˡ���ǯ�֤μ���Ψ��ҤȤ����ʲ��μ��Τ褦�ˣ����Ĥη�ּ���Ψ�ʣ������������ġ��������ˤ��¤ȹͤ��ޤ���
���ҡ�����ܣ����ܡġܣ��������ʣ�������
�����ǡ���ּ���Ψ��ʿ�ѡʴ����͡ˤ�̤Ȥ���ȡ���Ψ�ѿ����¤δ����ͤθ������顢ǯ�ּ���Ψ��ʿ�ѡʴ����͡ˤϣ����̤ˤʤꡢ��ּ���Ψ��ʬ��������Ȥ���ȡ���Ω�ʳ�Ψ�ѿ����¤�ʬ���θ������顢ǯ�ּ���Ψ��ʬ���ϣ��������ˤʤ�ޤ���������ϡ�ñ���DZ��Ѥ������Ǥ���
- ��Ψ�ѿ����¤δ����ͤθ���
- �šʣءܣ١ˡ�šʣءˡܣšʣ١�
- ��Ω�ʳ�Ψ�ѿ����¤�ʬ���θ���
- �֡ʣءܣ١ˡ�֡ʣءˡܣ֡ʣ١�
�ʤ���ʣ���DZ��Ѥ������ˤϡ��¤ǤϤʤ�����Ω�ʳ�Ψ�ѿ����Ѥ���Ѥ��뤳�Ȥˤʤ�褦�Ǥ�����ʬ���θ����ϳ�ǧ�Ǥ��Ƥ��ޤ���
- ��Ω�ʳ�Ψ�ѿ����Ѥδ����ͤθ���
- �šʣأ١ˡ�šʣءˣšʣ١�
- ��Ω�ʳ�Ψ�ѿ����Ѥ�ʬ���θ���
- �֡ʣأ١ˡᡩ
�����ȥꥹ�� (2009-12-11)
�ޤ������Ѽ���Ψ�ˤĤ��ơ�̤��γ�Ψʬ�ۤϤ狼��ޤ���ʿ�Ѥ�ɸ���к����������ʤ����⤷��ޤ���������������ꤷ�ơ�ʿ�Ѥ�ʿ�ѥ����ɸ���к���ꥹ���Ȥ��Ƥߤޤ���
�����ǡ�Ʊ��ʿ�ѥ����Ǥ���С��ꥹ�����㤯�������Ȥ����Ǥ�����Ʊ���ꥹ���Ǥ���С�ʿ�ѥ�����⤯�������Ȥ����Ǥ�����ʿ�ѥ���⤯�ƥꥹ�����㤤���Ѥ����褦�Ǥ���
�ʤ���������֥ϥ����ꥹ�����ϥ��������פˤĤ��Ƥϡ��ꥹ�����⤤���Ѥ�ʿ�ѥ���⤯�ʤ�Ȥ������ȤǤϤʤ���ʿ�ѥ���⤤���Ѥϥꥹ�����⤯�ʤ�Ȥ������ȤǤ���
ʿ�ѥ����ȥꥹ��
��ʿ�ѥ����
|
������
|
������
|
��ʿ�ѥ����
|
������
|
������
|
|
��ꥹ��
|
��ꥹ��
|
�ޤ���ʣ�������ˤĤ��ơ��֥���������Τγ���Ĺ�����Τ�����ס����ԡ�������ߡ����������롢���ԡ����⼣����������ǯ������������裲���ˤΣ����ڡ���������Ѥ��ޤ���
��ʣ�������ϻ��ѥ����ǯΨ������ʬ��������Ⱦʬ���������Ρ�����������ݣ�����������
�����Ȥ�ʣ��������Ĺ����ã���Ǥ��롣ʣ�������Ͼ�˻��ѥ�������㤤��
�����ǡ��ֻ��ѥ����פ�ʿ�ѥ����ǯΨ������ʬ�������פ�����ʿ������ꥹ���Ȥ���ȡ����Τ褦�ʴط��ˤʤꡢ�㤨�С�ʿ�ѥ������ꥹ������Ȥ��ơ�ʣ��������������ȡ�����ʡᣰ�����ݣ������������ˤˤʤ�ޤ���
- ʣ��������ʿ�ѥ����ݥꥹ��������
Credit
(C) 2007-2010 Yana
Direction: Yana
HTML: Yana
Program: Yana
ChangeLog
2010-12-11 release 17
2010-10-11 release 16
2010-08-11 release 15
2010-06-11 release 14
2010-04-11 release 13
2010-02-11 release 12
2009-12-11 release 11
2009-10-11 release 10
2009-08-11 release 9
2009-06-11 release 8
2009-05-11 release 7
2008-01-11 release 6
2007-12-11 release 5
2007-11-11 release 4
2007-10-11 release 3
2007-09-11 release 2
2007-08-11 release 1
2007-07-11 release 0
(C) 2007-2010 Yana
���Υ����ȤˤĤ���
